Análisis ANOVA: Inferencias
Para entender el comportamiento de una característica que puede ser afectada por una o múltiples variables. se debe establecer un modelo que nos permita evaluar si existe o no relación entre el resultado (Y) que buscamos obtener y los potenciales factores (X) que impactan significativamente en el comportamiento de la variable dependiente.
De tal manera que podamos establecer una hipotesis ( X →Y).
La lógica de la estadística inferencial consiste en partir de la información de una muestra para entender y predecir el comportamiento de una población.
Las pruebas de hipótesis son utilizadas ampliamente como parte del proceso de investigación, así como en la metodología Six Sigma ( Fase: Analizar) con el objeto de entender la causa que origina que un producto o servicio esté fuera de especificación.
A continuación se desarrollarán los siguientes ejercicios para comparar los resultados de una variable afectada por diferentes métodos.
Ejemplo 1:
Se realizó un experimento con germinado de semillas, el cual tenía por objeto determinar el contenido de proteínas de diferentes especies. El experimento se realizó con un diseño completamente al azar, obteniéndose los siguientes resultados:
¿Existe una diferencia en el contenido de proteína en las diferentes especies?
Se considerará un nivel de significancia del 5%
En primer lugar se determinarán los estadísticos de cada grupo de especies, para utilizar la información en nuestros cálculos.
A continuación planteamos la hipótesis nula y alternativa:
Ho: U1 = U2 = U3=U4=U5=U6 (En promedio el contenido de proteínas en todas las especies es el mismo)
H1: Al menos una de las especies difiere en el contenido de proteinas respecto de las otras especies.
Vamos a asumir de que se cumplen las condiciones para realizar el análisis ANOVA.
-Es decir cada muestra que representa una población es obtenida de manera independiente.
-La varianza es homogénea para todas las especies.
- La distribución de los datos de cada muestra se puede representar con una curva de campana ( Distribución normal).
Teniendo en cuenta estos principios a priori procedemos al cálculo del estadístico f.
Suma de Cuadrados Totales = Σ (Yi - Y ) ^2
Donde:
Yi: Valor de cada observación
Y: Media de Medias de la variable de respuesta
SCT = (5.13 - 3.12)^2 + (4.17-3.12)^2 + ....+ (3.32 - 3.12)^2
SCT = 63.24
Suma de Cuadrados de la Regresión = Σ nj (Yj - Y)^2
Donde:
Yj: Valor promedio de cada especie
nj: El tamaño de muestra de cada especie
Y: Media de Medias de la variable de respuesta
SCR= (6x(2.36-3.12)^2) + (6x(4.51-3.12)^2) + .... (6x(3.93-3.12)^2)
SCR= 54.47
Suma de Cuadrado del Error = SCT - SCR = 8.77
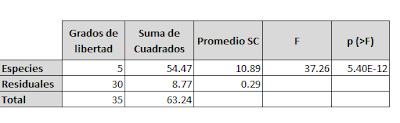
Ahora corresponder establecer la tabla ANOVA con los datos que se han calculado.
Para hallar los grados de Libertad asociados con ANOVA
Grados de libertad del grupo de la regresión = K -1 = 6 -1 = 5
(Donde K = nro de especies)
Grados de Libertad del total = n -1 = 36 -1 = 35
(Donde n= total de datos)
Grados de Libertad de los residuales = GLT - GLR = 35 - 5 = 30
- Para hallar el promedio de la suma de cuadrados, se divide cada suma de cuadrados entre los grados de libertad respectivo.
- Para hallar el estadístico F se divide el promedio de Suma de Cuadrados del grupo de la regresión entre el promedio de suma de cuadrados de los residuales.
Para un nivel de significancia del 0.05, considerando los grados de libertad del numerador 5 y del denominador 30. Se revisa la tabla de fisher que el valor de F es 2.53
Nuestro f calculado es 37.26 que estaría en la zona de rechazo , dado que este valor es mayor al f de tabla. (2.53)
Se rechaza la hipótesis nula y por tanto concluimos que al menos una de las especies tiene en promedio, mayor o menor contenido de proteinas.
Para identificar cual de las especies tiene una diferencia significativa frente a las otras se debe realizar una prueba de hipótesis con el estadístico t para comparar cada par de especies.
Ejemplo 2:
Se realiza un experimento para determinar el efecto de tres métodos de preparación del terreno sobre el crecimiento de pinos en el primer año. Cuatro localidades fueron seleccionadas y divididas en tres parcelas cada una. Como se esperaba que la fertilidad del terreno fuese más homogénea dentro de una localidad que entre las localidades, se utilizó un diseño de bloques aleatorios, tomando a las localidades como bloques. Los métodos de preparación fueron A ( ninguna preparación), B ( fertilización ligera), C (fertilización fuerte). Las preparaciones del terreno se aplicaron al azar a las parcelas dentro de cada localidad. En cada parcela se plantó la misma cantidad de árboles y se observó el crecimiento promedio durante el primer año de los árboles en cada parcela.
Realizar un análisis de varianza y verificar si existe evidencia de una diferencia significativa entre los crecimientos medios correspondientes a las tres preparaciones y entre localidades.
Respecto a las tres preparaciones:
Ho: U1=U2=U3 ( La media de crecimiento para las tres preparaciones es la misma)
H1: Al menos una de las tres preparaciones del terreno tiene una media de crecimiento diferente
Se analizará en Minitab si existe una diferencia significativa entre las tres métodos de preparación del terreno.
Para ello registramos los datos en función del tipo de preparación tal como se muestra:
Luego realizar click en el menú Estadística / ANOVA / Un solo factor (Desapilado) y se mostrará una ventana que nos permitira seleccionar las respuestas que queremos analizar de cada columna y el nivel de confianza es de 95%:
Finalmente damos click en Aceptar y aparecerán los siguientes resultados para interpretar:
Como se muestra en los resultados el valor de P es 0.152 de acuerdo a la tabla ANOVA
Considerando un nivel de significancia de 0.05 (alpha)
Interpretación
Si el valor de p < alpha se rechaza la hipótesis nula
Si el valor de p > alpha se acepta la hiótesis nula
En este caso p > alpha , por lo tanto podemos afirmar que no existe una diferencia significativa entre los métodos de preparación.
La media de crecimiento es el mismo , independiente del metodo de preparación del terreno.
Respecto a las localidades:
Ho: U1=U2=U3 ( La media de crecimiento para las cuatro localidades es la misma)
H1: Al menos una de las cuatro localidades tiene una media de crecimiento diferente
Realizamos el mismo proceso en minitab:
Finalmente obtenemos los siguientes resultados:
Interpretación:
Considerando un nivel de significancia de 0.05 ( Dado que seleccionamos como nivel de confianza 0.95)
p > alpha
Por tanto se acepta la hipótesis nula , es decir no hay un diferencia significativa respecto al crecimiento , independiente de la localidad.
En conclusión podemos afirmar que la fertilidad de los terrenos es homogénea.