Simulación de Montecarlo en R (Introducción)
Este método permite obtener resultados bajo diversos escenarios. Desde problemas cotidianos hasta fallas críticas en los procesos pueden ser anticipados a través de la simulación de Montecarlo.
El modelo se basa en el uso de variables aleatorias (estocásticas) para determinar el comportamiento de un fenómeno, proceso, producto, servicio, entre otros.
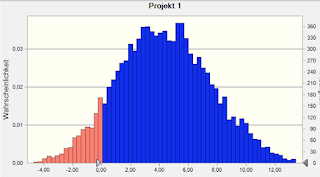
La data resulta ser un pilar importante para estudiar y analizar el comportamiento de una población, es por ello que resulta vital obtener datos que puedan ser medibles o contabilizados. Una frase que suelo utilizar es la siguiente: "No se puede mejorar aquello que no se mide."
La opinión o parecer de una persona no es determinante a la hora de afirmar categóricamente sobre un hecho. Son los datos , quizás números fríos los que revelan la situación o resultado de una linea de acciones que ha desarrollado un grupo humano, un proceso, una industria y hasta un país.
La necesidad de contar con data es crucial a la hora de usar modelos matemáticos para predecir el éxito o fracaso de un proyecto y en general de la sociedad.
A continuación se utilizará el software R Studio como herramienta para desarrollar la simulación de Montecarlo, teniendo data colectada en el inicio de este ejemplo.
Peso esperado de ratones
Se ha desarrollado una dieta especial para ratones. Se espera que los ratones adultos obtengan un peso promedio de 26 gramos.
1. En primer lugar se extrae la data almacenada del archivo con extensión CSV (225 datos correspondiente al peso de ratones) (Ítem 1) y se convierte los datos en un vector llamado "peso" (Ítem 2)
2. Se crea la función "generator" (Ítem 3) que va a crear la muestra aleatoria con tamaño "n" (por definir)
3. Se crea el parámetro "test" que replicará el modelo (1000) veces , utilizando una muestra de tamaño 30 (Ítem 4) y se grafica los resultados en un histograma con la función hist() (Ítem5)
4. Utilizando una muestra de 30 datos se muestra el Histograma 1
5. Utilizando una muestra de 50 datos se muestra el Histograma 2
6. Utilizando una muestra de 100 datos se muestra el Histograma 3
Como se puede apreciar mientras más datos se utilizan, la distribución de los pesos sigue una curva normal que se acerca al valor de 24 g., lo que indica de forma gráfica que la mayoría de ratones pesa menos de 26 g (Objetivo) e implica modificar la dieta para lograr el objetivo.
Si bien podemos calcular el promedio de los datos de manera directa (23.89 g) este ejemplo introductorio nos señala un principio básico. Tomar una muestra representativa nos ayuda a predecir el comportamiento de la población. Esto claramente lo vemos en el modelo de Montecarlo al replicar 1000 veces la simulación con diferentes tamaños de muestra se observa claramente que mientras el tamaño de la muestra es significativo existe mayor precisión en los datos.















