Teorema de Bayes - Predecir el comportamiento de una acción de bolsa

Si recurrimos a la teoría de la probabilidad sabemos que:
P (A y B) = P (A/B)*P (B)
La probabilidad conjunta de que suceda A y B es igual a la probabilidad de que suceda A dado que se cumplió B, por la probabilidad de que suceda B.
P(ByA) = P(B/A)*P(A)
La probabilidad conjunta de que suceda B y A es igual a la probabilidad de que suceda B dado que se cumplió A, por la probabilidad de que suceda A.
Si igualamos ambos enunciados:
P (Ay B) = P(By A)
P(A/B)*P(B) = P(B/A)*P(A)
Entonces tenemos el enunciado de Bayes:
P (A/B) = [P (B/A) * P (A)] / P(B)
La probabilidad de que suceda A dado que se cumplió B, es igual a la probabilidad de que suceda B dado que se cumplió A por la probabilidad de que suceda A, dividido entre la probabilidad de que suceda B.
Tomando en consideración estos enunciados vamos a calcular la probabilidad de que las acciones de Tesla (TSLA) aumenten su valor en los próximos días:
1) En primer lugar debemos establecer la relación de dependencia entre dos variables , para nuestro caso las acciones de Tesla (TSLA) comparadas con el indice bursatil referente Vanguard S&P500 (VOO) a fin de demostrar estadísticamente que existe una alta relación lineal entre ambas acciones de bolsa.
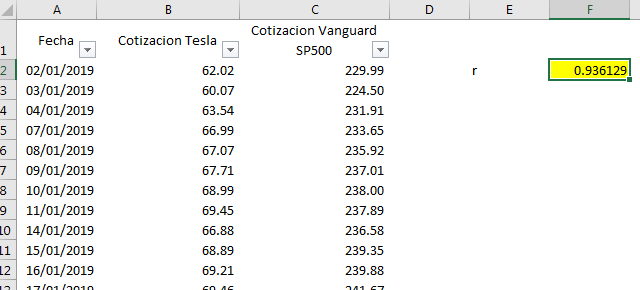
- Se muestra el extracto del histórico de cotizaciones diarias de las acciones de Tesla (TSLA) y Vanguard S&P500 (VOO) considerando el periodo 02/01/2019 hasta el 07/01/2022.
- Utilizando la fórmula de excel se calcula el coeficiente de correlacion (Pearson) (=COEF.DE.CORREL(Matriz1, Matriz2) ), siendo el resultado 0.9358 , lo cual indica que existe una alta dependencia lineal positiva entre ambas variables.
- En el siguiente gráfico de dispersión que compara ambas variables podemos evidenciar visualmente, que mientras las cotizaciones de Vanguard S&P500 se han ido incrementando a lo largo del tiempo, lo mismo ocurre en el caso de las acciones de Tesla (TSLA).
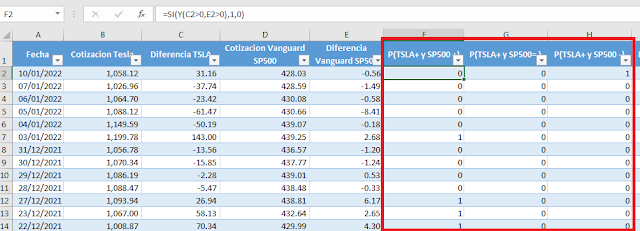
2) Ordenar la cotización de las acciones de forma descendente (de la fecha más reciente a la más antigua), seguido calcular la variación de las cotizaciones simplemente restando el valor de la cotización del día contra el día anterior, aplicar la misma operación en ambas acciones de bolsa.
3) Calcular la frecuencia o número de veces que las acciones de:
- TSLA suben y VOO tambien suben
- TSLA sube y VOO se mantiene igual
- TSLA sube y VOO baja.
4) Calcular la frecuencia o número de veces que las acciones de:
- VOO suben
- VOO se mantiene igual
- VOO baja

5) Se muestra el resumen de los resultados en la siguiente tabla dinámica:
6) A continuación se va a ordenar en la siguiente matriz los resultados obtenidos:
Por ejemplo:
- En la casilla que corresponde a las acciones de TSLA aumentan y VOO aumentan colocamos 288 que viene a ser el número de veces que se cumple la condición durante el periodo analizado.
- El número de veces que VOO aumenta es 437 , colocamos este valor como total de la fila.
- La suma de cada casillero de una fila de la matriz debe ser igual al total de la fila correspondiente.
288 + 149 = 437
416+ 346 = 762
7) Para calcular la probabilidad de que las acciones de Tesla (TSLA) aumenten, calculamos la suma de la columna que corresponde a la condición "acciones de TSLA aumentan", seguido lo dividimos entre el total de cotizaciones (762).
P (TSLA +) = (288 + 2 + 126) / 762 = 55 %
Conclusión: Podemos afirmar de acuerdo a la información histórica y tomando en consideración el teorema de bayes, existe un 55% de probabilidad de que las acciones de Tesla sigan aumentando su valor en los próximos días.
Otra ventaja de esté método es que la información obtenida puede ser actualizada con información real de nuevas cotizaciones, lo cual modifica los resultados de la probabilidad según el comportamiento real de la acción.